[雑感044] 統計が専門ではない教育関係者にとってできるだけ分かりやすいベイズの定理の説明

を試みる。手っ取り早く説明を読みたい人は、（前置き）を飛ばして（ここから説明）を読まれたし。今まで見た範囲では、

• エリオット・ソーバー（松王 政浩(訳)）(2012).『科学と証拠: 統計の哲学入門』名古屋大学出版会.

の例が分かりやすいので、少し借りた（特にpp. 14−17）。

（前置き）

先日、東京大学社会科学研究所CSRDA主催の計量分析セミナー2016・夏「はじめての統計データ分析: ベイズ的〈ポストp値時代〉の統計学」を受講した。丁寧に時間どおり一つひとつのステップを辿り、どんな質問にもきちっと誠実に答えようとする豊田先生のお姿に同じ「大学教員」として我が身を恥じるばかりであったのはさておき、早稲田大学での講義ノートをまとめ整えた

• 豊田 秀樹 (2016).『はじめての統計データ分析: ベイズ的〈ポストp値時代〉の統計学』朝倉書店.

の講義で、贅沢にも著者本人が解説をしてくれるわけだから、独りでこの本を読むより随分わかりやすかった。わかりやすかったのだが、では同じ解説をして自分の学生・院生、あるいは小中高の先生がたにベイズ（的考え方）を受け入れてもらえるかというと、そうは思えなかった。「ハミルトニアンモンテカルロ法によるMCMCは難しい」といった、そういう、ちゃんと使おうと思ったらある程度難しいのは当然だし実際に手を動かしてみよというレベルの話ではなく、導入やそもそもの考え方のところでまだずいぶん距離がある感じがした。

例えばベイズの定理のところで、この講義では身長と体重を例に条件付き分布を説明していたのだが、この時点ですでに落とし穴がある。多くの人は、というよりも統計を専門としない人の大半は、身長と体重の関係を確率分布として考えてはいないからだ*1。

加えて豊田 (2016)は、架空の「牛丼問題」から始まる。これも微妙で、どれくらいの学生・院生が、飲食店が提供する商品の量、つまり品質管理の問題として牛丼を見たことがあるだろうか。5gの差は–そもそもこれまでの人生で牛丼を注文して、上に乗っている具を「グラム」で考えたことはないのだが–企業的には品質や大局的なコストの問題として無視できないところだろうが、バイトで牛丼に接する学生にとって理想とされる水準への近似は自分の経験と技量の問題でしかなく、客にとっては感覚的な満足度の問題でしかない。牛丼屋が実際に一杯一杯の牛丼を秤に載せて目盛りを確認してから客に出しているのか分からないが、実際に数値が登場する例としては、デパ地下などのお肉屋の量り売りが浮かぶ。複数回利用していれば確かに200gをズバッと掴むベテランもいれば、粗っぽいところから刻んで合わせてくる新人もいて、誤差の存在は実感できる。しかし、ここの店員さんも「上手くなってきた」とか「今日は調子が悪い」と思うことはあっても、「何割の確率で客が求める量より10g多く売っている」といった考え方はおそらくしていないだろう。要するに、挙げられている例は具体的だが、日常で実際にそういうことを考えるかどうかという点で見ると多くの人にとっては現実的ではなかったり、その立場に立つ人が特殊で実際的でなかったりする*2。教育方法学という専門上、あるいは性格的に、こういうのが気になるのだ。

もちろんこれはベイズ（的考え方）に限った問題ではなく、いわゆるハンバーガー統計がまさにそうだった。他店のポテトのほうが短かろうが長かろうがわれわれはそんなことは気にせずポテトをモグモグしてきたわけで、このエピソードにあやかってモスに対してもっとマックっぽいポテトを出せと文句をつけた客がいたとは考えにくい。仮に–それで何か商売上の価値が出るとは全く思えないが–「他店のポテトと同量です！」と宣言してそこに文句をつける客が現れた場合、現実は、ポテトの長さを測り平均値を計算して比べることなどせず、返金するかポテトを数本足したり引いたりするかして解決するだろう（経営者側は裏で検証作業をするかもしれないが）。必ずしも全てを完璧に満たす必要はないが、文脈が複雑になったり不自然さが増してしまうぐらいなら、できるだけシンプルな例が良い。

記述統計や帰無仮説検定については、教育心理学はもちろん、外国語教育についても研究の蓄積は多くあり、自分のほうの理解もだいぶこなれてきたところがあるので、なるべく（英語）教育に引き寄せ、なるべく現実的で実際的な例を挙げようと努めてきた。しかし帰無仮説検定の考え方や手順の様々な不自然さを乗り越えてもらうのに疲れてきたこともあるし、乗り越えたら乗り越えたで、どれだけ防ごうとしても「ピー値ウェイ！有意ウェイ！」みたいな姿を見て悲しくなることも少なくないので、豊田先生と同じ内容・水準は1000回生まれ変わっても無理（p < .001）だとしても、少しずつベイズ（的考え方）に移行できないかと思って上記セミナーを受講したのだが…（前置き冒頭に戻る）。

ということで、その前からベイズ統計学の本をちらちら読んでいても気になっていたのだが、ここまで述べてきたような痒さをわかって解説してくれる例にほとんど出会わない。じゃあ素人なりに考えて書くしかないか。間違っていたら専門の人がちゃんと教育して叱ってくれるだろう。

• 浦野 研・亘理 陽一・田中 武夫・藤田 卓郎・髙木 亜希子・酒井 英樹 (2016).『はじめての英語教育研究: 押さえておきたいコツとポイント』研究社.

を上梓しても思った（こちらを参照）ことだが、それがうまくいったとしたら、いつか「授業研究・授業実践のための統計学」としてまとめたい。とは言えそれは、浦野・亘理・田中・藤田・髙木・酒井 (2016)の第6章があったとしても、分散とは何ぞや、何のためにどういうリクツで出すものナリかといったところから始まる気がするので、この辺の話は随分あとになるのかもしれないけど。

 

（ここから説明）

トランプを一組用意する。ジョーカーや予備のカードは抜いて、よく切って、一番上のカードを一枚引く。カードのマークはなんだろうか。当ててみよう。BGMはStingのShape of My Heartがいい。I love you too, Leon.

イカサマは無しとして、ハートが出る確率はどれくらいだろうか。一つのマークにつきカードはAからKまで13枚あって、マークは4種類、つまりジョーカーを除いたトランプは52枚ある。52枚中の13枚がハートだから1/4、あるいは今は1枚引けば必ず4種類のうちのどれかに当たるので、4種類のうちのひとつということでそのまま1/4。ゆえにトランプを一枚引いてハートが出る確率は25％。数学の人たちは確率をPとかPrで表すので、

P(♡) = 1/4

と書いてしまおう。PはProbabilityのピー。

「4回に1回は当たるってことを小難しく書いただけじゃねえか」と思った人は、このゲームを12回やってみんしゃい。規則的に（例えば2回目、6回目、10回目で）3回当たっただろうか。そうなることもあるだろうが、大方の場合そうはならない。何回目に当たったかを問わなければ3回になる人が多いかもしれないが、2回しか当たらなかった人も4、5回当てた人もいるだろう。1回も当たらなかった人は…まあギャンブルはやめておいたほうがよさそうだ。いま「ギャンブル」と言ったが、ギャンブルはまさにこの予想の当たり外れを利用して成り立っている活動だ（実際には心理戦の側面が大きいとしても、そもそも必ず負けると分かっていて金品を賭ける人はいない）。予想に当たり外れがある、難しく言うと偶然性があるということだが、これが、P(♡)=1/4が「4回に1回は必ず当たる」という規則ではなく、確率を表しているということの意味だ。

だから1/4という数値は、上に書いたように、52枚中の13枚だから、もしくは4種類のうちのひとつだからという情報から計算して導き出した、われわれがトランプを引く前に期待している値である。これを事前確率という。実際にトランプを引く前に予想したり計算したりしている確率という意味ね。

では同じくトランプを1枚引いた時、そのカードが絵札(J, Q, K)である事前確率はどうか。P(絵札)だ。各マークに3枚ずつ絵札があるから52枚中12枚、つまり、

P(絵札) = 3/13

だ。

さて、一人で当たった！外れた！と繰り返していて危ない人と思われても困るので、ちょっとディーラーと勝負してみよう。10回勝負で3回以上カードのマークを当てればあなたの勝ち。7回以上外せばディーラーの勝ち。事前確率的にはちょっとあなたの分が悪いようにも思える。ところが、このディーラーがなかなかのヘッポコで、あなたにチロッと次のカードを見せてしまった。マークや色までは見えなかったが、数字札ではなく絵札であることが確認できた（つまり3/13の確率で起こるP(絵札)を観察した）。あなたはきっと心の中で「おいおい、オービー君、敵に塩を送っちゃいかんよ」とほくそ笑んだかもしれない。さて、確率的にはどうだろう。あなたは次のカードはハートだと思っている。絵札が見えて、ハートである確率は果たしてあがったのかさがったのか。

確率は一般に、

P(♡) = {♡}/{♡, ♢, ♠︎, ♣︎}

というように、

P(そうなる)=(そうなる場合の数)/(そこであり得る全ての場合の数)

で計算するので、「絵札が見えた時にそれがハートである確率」も、絵札＆ハートである確率を、絵札である確率で割れば求めることができる。あまり難しく考えなくても、いわゆるベン図で整理すると関係が見えやすい。

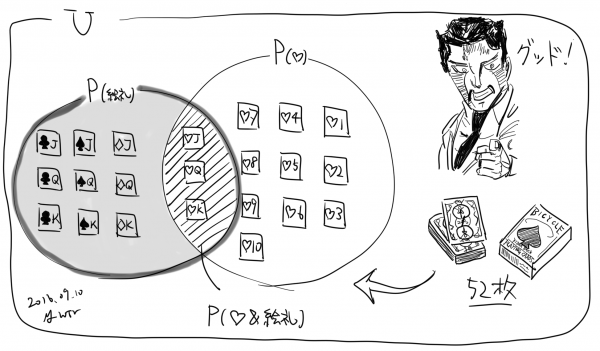
ここでのそうなる確率は「絵札＆ハートの確率」。つまり、

P(絵札＆♡) = 3/13 × 1/4 = 3/52

で、トランプを1枚引いた時に絵札である確率は上で求めたように3/13だ。上のベン図で左側の円の中に占める真ん中の3枚を考えても同じことだが、したがって、実際この場面で次のカードがハートである確率は、

P(絵札が見えた時にそれが♡) = P(絵札＆♡)/P(絵札) = 1/4

となり、確率的にはP(♡)と変わらない。それは、あるカードが絵札であることと、そのマークがハートであることは独立した事象だからだ。つまり、どのマークにも同じ数だけ絵札があるし、どの絵札にも4種類のマークがあるということ。独立していない例としては、マークの色と種類の関係を考えてみるとよい。ディーラーがうっかりポロリした時に確認したマークが赤色だったなら、それがハートである確率は倍に跳ね上がるわけだ。

さて、「絵札であることが見えた時にそれがハート」というのを数学の人たちは縦棒を使って、縦棒をギブンと読んだりして、

P(♡|絵札)

と表記する。順番が入れ替わっただけの気もするが、あくまで気になっているのは先にあるハートである確率で、絵札であるのは既に与えられた（given）条件ということを言わんとしている。カードが絵札だという条件が与えられた事後にハートである確率、という意味で事後確率という。

ここからが特に数学の人っぽい考え方を要するのだが、この縦棒の考え方を当てはめて、

P(絵札|♡)

というのを考えてみる。つまり「引いたカードがハートだった時にそれが絵札である確率」。上のベン図を見てもらえれば、それはハート13枚中の3枚だから、3/13だということがわかる。先ほどと同じように求めれば、

P(♡を引いた時にそれが絵札) = P(♡＆絵札)/P(♡) = 3/13

というわけだ。この、「カードがハートだった時にそれが絵札である確率」を尤度という。「尤」は「もっともらしい」という意味だが、独立事象だとピンとこないので、ちょっと別の例で考えてみよう。

例えば、賞味期限の切れた牛乳を飲んだ時にお腹が痛くなるかどうかは、偶然性があると考えられる。世の中には胃弱ゥ極まりない人もいれば鉄の胃腸を持った人もいて、必ずお腹が痛くなると決まったわけではないからだ（個人的には100％外れなくお腹を壊しそうだけど）。さて、この「賞味期限の切れた牛乳を飲んだ時にお腹が痛くなる確率」を事後確率と考えた時、「お腹が痛い時に、それが賞味期限の切れた牛乳が原因だったと言える確率」が尤度となる。この場合、事後確率は感覚的にも高そうだが、尤度はそうとは言えないことがわかるだろう。なぜなら、賞味期限切れの牛乳は確かに尤もらしい犯人ではあるが、お腹が痛くなる原因は他にもたくさんあるからだ。昨夜の生肉や寝冷えやストレスや…ああ現代社会にはなんて多くのポンポンペイン要因！*3 そういう要因が自分に多くある時、賞味期限切れの牛乳が原因である尤度は低いが、毎日の生活リズムは安定していてストレスもないし病気もしてないという場合、先ほど飲んだ牛乳が原因である尤度が高くなってくる。そういう風に、観察されたことが成り立ちやすい場合はどういう場合かということをあれこれ考えるので尤度と呼ばれるわけだ。（当たっているかどうかは別として）日常的に観察したことの辻褄合わせとしてわれわれがよくやっている推論（アイツまた新車買ったらしい→宝くじでも当たったのかな）を考えてみれば、実は尤度的な発想はごくありふれたものであることがわかる。

P(♡|絵札) = P(絵札＆♡)/P(絵札)　　　（#事後確率）

P(絵札|♡) = P(♡＆絵札)/P(♡)　　　　（#尤度）

事後確率と尤度の式を改めて並べてみよう。下線部が、絵札と♡の順序は入れ替わっているが、同じことを表現しているのに気がついてもらえるだろうか。要するにベン図で二つの円が重なっているところだ。ということは、数学的に考えると、上の2つの式はP(絵札&♡)=P(♡&絵札)を通じて繋ぐことができるということになる。

P(絵札&♡) = P(♡|絵札)×P(絵札)　　　（#事後確率式の変形）

P(♡＆絵札) = P(絵札|♡)×P(♡) 　　   　（#尤度式の変形）

なので、

P(♡|絵札)×P(絵札) = P(絵札|♡)×P(♡)   （#２つの式をつないで）

となり、ついには事後確率を

P(♡|絵札) = P(絵札|♡)×P(♡)/P(絵札)    （#両辺をP(絵札)で割る）

と表現することができる。これがベイズの定理だ。念のためこれまで計算してきた確率を代入してみると、

P(♡|絵札) = 3/13×1/4／3/13 = 1/4

で計算も合う。つまり、ベイズの定理とは、

P(事後確率) = P(尤度)×P(事前確率)/P(観察)

ということで、ものすごく感覚的に表現するなら、

こうだった時にどうなの = それだったと言えそ×どうなると予測/こうだった！

という関係を表していると考えることができる（ワタリ的ベイズ理解）。

トランプ遊びが過ぎた。われわれにとって重要なのは、これを教育に当てはめると何が言えそうかということだ。ここから先の道のりは長いのだが、さしあたりこんな例を考えてみよう。

今リーアム・ニーソンが静岡駅に降り立った。バスで静岡大学に行きたいのだが乗り場がわからない。人を殺傷することなく目的のバスに乗るにはどうしたらいいだろうか。そうか、道行く人に尋ねればいいのだ。この時、駅前を歩く人が彼の英語を聞き取って応答できるかどうかは偶然性がある。つまり、英語話者が道行く人に英語で話しかけてうまく対応してもらえる確率（リーアム・ニーソン問題, LN）として考えることができる。リーアム・ニーソンを基本とするのもどうかと思うが、ナイスミドルのイイ声は、言葉数は少なく端的だが、それほど聞き取りやすいとは言えないだろうか。実際は1/10ぐらいかな。でも今、高校生に限定して、5人に1人は対応できることを期待してみよう。がんばれニーソン、がんばれ静岡県民。

あなたは今、生徒がこのリーアム・ニーソン問題をクリアできる、つまり「英語話者に道を聞かれてその内容を聞き取って応答することができる」ようなリスニング・スピーキング指導をしたいと考えている。今年からそこを意識して選んだW社の教材（W）を導入したので、リーアム・ニーソン問題にどの程度有効かを知りたい。結果をどのように測定するのかはいつも悩ましいのだが、リーアム・ニーソン似のALTにロールプレイ的なタスクでテストしてもらって、生徒の熟達度を測ったとする。これを、W社の教材がうまくいっているかどうかの指標としよう。これを観察=データとして得た。この状況をベイズの定理に当てはめれば、

• 事後確率: W社の教材を使用した生徒がどの程度リーアム・ニーソン問題をクリアできるか（P(LN|W) ）
• 尤度: リーアム・ニーソン問題をクリアできた人のW社の教材使用率（ P(W|LN)）
• 事前確率: 一般的なリーアム・ニーソン問題の予想通過率（P(LN)）
• 観察=データ: ロールプレイ的なタスクの結果（P(W)）

と整理できる。

P(LN|W) = P(W|LN)×P(LN)/P(W)

ここで問題となるのは、P(W|LN)がP(W)と同じ、つまりトランプの例と同じように尤度が観察と同じであれば、事後確率は常に事前確率と一致してしまうということだ。例えば、事前確率が上に示したように1/5で、このクラスでは4人に1人がロールプレイ的なタスクをクリアできたとしても、上の式で計算する限り事後確率は1/5になる。実際25％が成功しているのに20％という予測がはじき出されては納得もいかない。何かがおかしいのだ。これは、観察したデータのみで尤度を計算していることによる。観察したことは事実だが、リーアム・ニーソン問題をクリアできた人で（もちろんできなかった人も）W社の教材を使っている人は他にもたくさんいる。このクラスに限って言えば、全員がW社の教材を使っているのだから、タスクをクリアできた人の割合がすなわち尤度になってしまうのは当たり前のことだ。

なのでベイズの定理（的考え方）に基づく推定（ベイズ推定）では、先ほどの牛乳腹痛の例のように、尤度を様々な可能性がある分布として考える。つまり、手元のデータをもとに予測しようと思ったら（このタスクの結果がW社の教材のリーアム・ニーソン問題への効果を正しく示しているとしたら）、W社の教材の使用率がどうであればリーアム・ニーソン問題の成功率を最もうまく説明できるかということをゴニョゴニョ考えるのだ。

さらに言えば、実際には例えばこちらの2枚目に示されているように、生徒の英語運用能力もある程度の広がりをもって分布している。文科省の調査例のように連続した量で分布していると考えるか、できるかできないかのゼロイチで考えるかは測定法の問題だが、日本全国の高校からランダムに選ばれた生徒はこの分布のどこかに落ち着くと考えられる。冒頭のトランプの例と同じように、5人に1人が必ずリーアム・ニーソン問題を通過するわけではなくて、10人選べば3人通過したり1 人も通過しなかったりするだろう。ポイントは、ベイズ推定では、事前確率（母数分布）は絶対に1/5だと予め決められるものとは考えないということだ（そもそも、予め事前確率がハッキリわかっている現実の事象がどのくらいあるのかわからない。賞味期限の切れた牛乳による腹痛の事前確率など聞いたことはない）。それが1/5だという「真理」を確かめようとしているのではなく、むしろ、リーアム・ニーソン問題の通過率が1/5だとすれば、あるいはそれを1/4にするためには、W社の教材で授業を受けた生徒はどのくらいタスクに成功しなければならないか、というようにゴニョゴニョムニョムニョ考える。

とりあえず今のところは、得られたデータをもとに、その尤もらしさと未知の母数がどういう分布になるかについてあれやこれやと推測するのがベイズ推定だと言っておけばいいだろうか。だいぶややこしくなってきたように見えるが、われわれが授業を研究したり実践して改善しようとする時、「W社の教材を使ったクラスで以前よりうまくいかない確率は100回に5回以下です*4」と言われるよりは、得られたデータから推定すると、8割ぐらいの確信度で、以前のやり方のX倍の確率で目標を達成できると言えそう、ほとんどの生徒が前のやり方よりも伸びると言えそうなどと言われるほうが感覚的に納得しやすいし、教育(行為に対する評価)という現象の実態にも合っていると思うのだが、どうだろうか。

続きはまた今度。

To be continued…

 

*1 関連して、統計の入門書で、散布図の例に身長と体重が使われて「右肩上がりの傾向が確認できる」などと説明されることがある。これも、大規模に、確率分布的に考えれば、（幼児から大人への成長を考えても）身長が高くなればそのぶん体重も増えるんだろうと納得しはするが、これまでの経験で出会った人には、身長が低くてもズッシリ重そうな人やヒョロヒョロっと身長が高い人もいるので、あるいは自分を省みても、なんとなく腑に落ちなかったりする。実際、仮に散布図がそういうケースも含めて分布を示していたとしても、「右肩上がりの傾向」と言われた時、直線的で、固定的な法則をイメージする人が少なくないので、違和感が残る。そういう人たちが、回帰式や分散説明率をすぐ理解できるなら苦労はしない。

*2 そもそも、こういったことを超越したところで議論ができるからこそ数学や統計学だという気もするのでさじ加減は難しいところだ。経験的に言えば、二項分布から正規分布を導くときに、前田（kazutan）先生の例に倣って、W先生が週に2回の確率でチャーハンを食べるとして…という例は比較的受け入れてもらえる。この例の良さは一ヶ月、一年と拡張するときに、まあ毎週規則的に食べるわけじゃあるめえと誤差を理解しやすいことで、それでも週にn回チャーハンを食べる確率を求める作業については、週に2回チャーハンを食べるなら2回じゃないの？と最初は少なくない学生がなるので、この辺が限界かなと思う。

*3 一方、トランプの例に戻ると、ディーラーがチラッと見せたカードが赤だった時、それがハートのエースである事後確率は1/26だが、ハートのエースを引いた時それが赤いカードである尤度は1である。ハートのエースまで絞らないとして、赤いカードを見てそれがハートである事後確率は1/2だが、ハートを引いた時それが赤いカードである尤度はやっぱり1である。

*4 うまくいく・いかないの基準はいまは措くとして。